Using Math to Build the Ultimate Taffy Machine

When most of us see a taffy-pulling machine cranking away on a touristy boardwalk, we think of sweet, sweet sugar. Jean-Luc Thiffeault thinks of sweet, sweet math. As an applied mathematician at the University of Wisconsin-Madison, Thiffeault is particularly interested in the way materials like taffy get mixed: In the machine, the candy is stretched and folded over and over to incorporate air and develop its light, chewy texture. As it’s pulled, the original rectangle of taffy gets stretched more and more—its length growing exponentially by the same ratio each time. That stretch ratio is what interests Thiffeault. 

When a person pulls taffy, they’ll generally take the lump of candy and stretch it over a hook, bringing the two ends together. Then they’ll take that folded piece and stretch it over the hook again, doubling the length, and so on. In other words, “The human way of doing it is a multiplication factor of 2,” says Thiffeault. Mechanical pullers can do better, often yielding larger, exotic irrational numbers as their stretch factors.

It turns out that taffy pulling can be modeled by an abstract field of mathematics known as topological dynamics, essentially the study of long-term, large-scale changes over time in a mathematical space. (If the word topological sounds familiar, it was in the news recently as part of this year’s Nobel Prize in Physics.) The same mathematics that describes taffy-pulling also has more serious applications: many industrial processes, including glassblowing and drug preparation, require viscous fluids to be mixed in ways that are more like pulling taffy than stirring cream into coffee. “If you’re trying to stir really viscous things, like pharmaceutical industry pastes, you can’t just shake them,” says Thiffeault. “It’s not like mixing paint.”

Thiffeault has understood taffy-pulling as an example of viscous mixing for a long time, but only recently has he actually looked into the history of taffy-pullers to unearth their mathematical secrets. The result of that excursion into historical patents is his recent paper “A mathematical history of taffy pullers,” published on the preprint server arXiv in July.

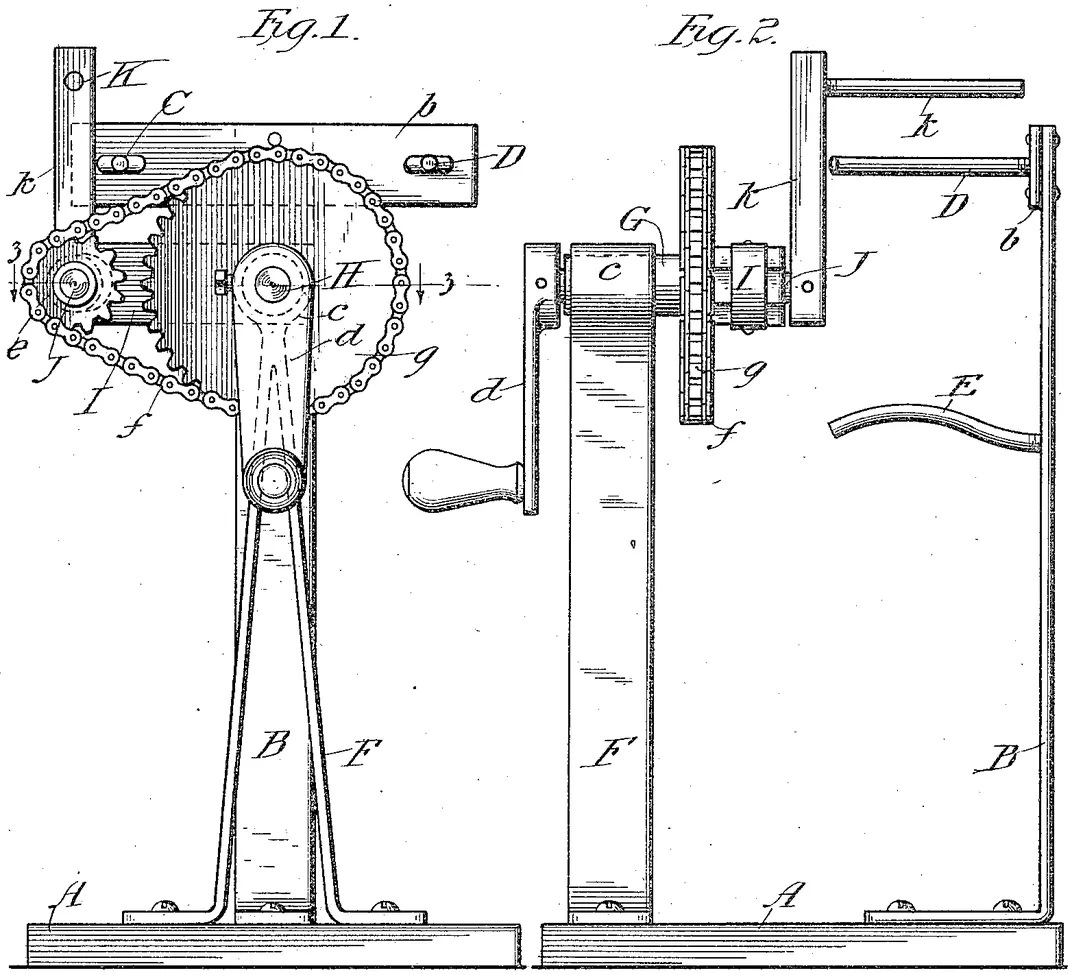
Specifically, the area that led to his taffy-puller deep dive is the study of what are called pseudo-Anosov mappings. Pseudo-Anosov is a fancy way of describing a process in which a two-dimensional shape is stretched exponentially in one direction while it shrinks in the other. Mathematically, the study of pseudo-Anosov mappings is relatively new. “In the ‘70s and ‘80s, people were trying very hard to find examples,” Thiffeault says. Ironically, they were there all along in patents for taffy-pullers. “Because mathematicians never looked at this literature, they would have never known they existed,” he says.

While he was combing through taffy-puller patents, Thiffeault stumbled on a legal battle that went all the way to the Supreme Court. At issue in the 1921 case Hildreth v. Mastoras was how broadly a 1900 patent for a taffy-puller should be construed. That is: was a later model made by someone else merely a minor improvement, or was it a different device? A crucial part of the argument was how different the 1900 patent was from an 1893 predecessor (which was probably never manufactured). The opinion of the court, authored by Chief Justice William Howard Taft, “shows a keen grasp of topological dynamics,” writes Thiffeault in his article.

The court recognized that the earlier device—which had only two hooks—could not have stretched the taffy to the exponential degree required for efficient confection creation. Taft’s opinion states:

With only two hooks there could be no lapping of the candy, because there was no third pin to re-engage the candy while it was held between the other two pins. The movement of the two pins in concentric circles might stretch it somewhat and stir it, but it would not pull it in the sense of the art.

Thiffeault writes, “The Supreme Court opinion displays the fundamental insight that at least three rods are required to produce some sort of rapid growth.”

Thiffeault says there are two standard taffy-pullers in use today, one with three rods and one with four. They happen to have the same stretch factor. It is related to the so-called silver ratio, 1+ √2, or about 2.414, a slightly less luminous cousin of the more famous golden ratio.

Six-pronged taffy puller

Watch on

The fact that the two standard taffy-pullers stretch with the silver ratio is interesting because the silver ratio is—in a precise mathematical sense—optimal. However, Thiffeault cautions that it’s not so easy to rank different taffy-pullers, even when you know their stretch factors: “There’s an apples and oranges aspect to it which is quite difficult to get around,” he says. One puller might have more rods and take longer to return to its initial state than another, or it might require more torque or more complicated gearing. So although mathematics does give some insight into how well taffy-pullers pull, it doesn’t tell the complete story.

Thiffeault’s research into taffy-pullers inspired him and his undergraduate student Alex Flanagan to build their own model. They wanted to see if they could increase the efficiency without modifying the gears much, and ended up making a novel 6-rod puller based on the gearing of the standard 4-rod puller. “The reason why we were able to do it is that we have math now,” Thiffeault says. They could model the machine extensively on the computer and bypass a lot of the trial and error with real physical devices earlier inventors had to do. The 6-rod device, which is still only a prototype, stretches taffy about twice as much as the standard pullers in each cycle.

So far, taffy-puller manufacturers haven't exactly been beating down Thiffeault’s door to get his advice on optimizing their designs—Big Taffy is apparently content with its stretchy status quo—but he has hopes that his methods could have effects in other industries. Besides glassblowing, one logical place for mixing optimization is the pharmaceutical industry. After all, mixing vitamins and drugs requires extremely high quality control: Manufacturers are "willing to pay a lot of money for perfect mixing" because they "can't tolerate one bad multivitamin out of 1000," says Thiffeault. So someday, pharmacists may be giving a sweet shoutout to the devoted taffy-pullers of yore.

Then again, that might be a bit of a stretch.