From Auto-Tune to Motor Oil, Pi Helps Power the World

March 14 is no regular Pi Day this year. Math enthusiasts everywhere are celebrating the event as Ultimate Pi Day, because the date will correspond to the first five digits of pi (3.1415) rather than just the first three. This mathematical confluence won't come around again for a century, on March 14, 2115.

Defined as the ratio of a circle's circumference to its diameter, pi (π) is both a transcendental and an irrational number, meaning it can never be written as the ratio of two whole numbers, and it continues indefinitely without any repeating pattern. Pi isn't the only irrational number—there's also Euler’s number (e) and the golden ratio (φ, or phi), for example. But it continues to be a source of fascination because its origins are easily explainable, says Mario Livio, an astrophysicist at the Space Telescope Science Institute in Maryland.

“Everyone can understand how pi is derived. All of the other numbers are more complex. The number phi, for example, involves a particular division of a line, and the number e requires you to know what a logarithm is,” says Livio, author of the book Is God a Mathematician?

Another big part of pi’s appeal is that it has an uncanny knack for appearing in mathematical formulas, many of which are important for everyday processes from image processing to GPS navigation. Here is just a small sampling of the commonly used formulas that include pi:

The Fourier Transform

Named for French mathematician Jean-Baptiste Joseph Fourier, this mathematical tool decomposes a signal into its component frequencies—rather like how a musical chord can be broken down into its component notes. In essence, Fourier transforms are ideal for processing wave-based signals such as sound or light and finding patterns. That makes the Fourier transform a fundamental tool in the modern digital world.

“It’s been called the single most important algorithm ever developed by mankind. Now that may be hyperbole, but maybe it’s not,” says Glen Whitney, founder and director of the National Museum of Mathematics in New York City. Fourier transforms are used all the time to clean up digital images, to Auto-Tune pop stars, and to find far-off planets orbiting other stars. The tool is also crucial for the voice-to-text features that are now standard on smartphones. “When you use Siri or Google Now, one of the first steps is to take your voice and do a Fourier transform on it … it turns out to be much easier to recognize vowels when you look at their Fourier transforms than when you look at the original signals themselves,” Whitney says.

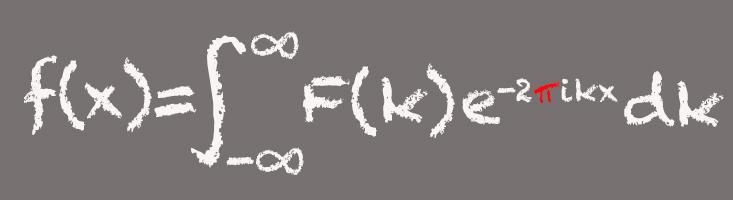
Pi appears in the Fourier transform because one of the component parts, or expressions, of the formula is associated with sine and cosine and the angles created by a particle traveling around a circle. “Whenever you have a formula that deals with circles or angles, you are not going to be surprised when pi shows up,” Whitney says. 

Heisenberg Uncertainty Principle

One of the pillars of quantum mechanics, Heisenberg’s uncertainty principle states that an observer can't know both the position and speed of a subatomic particle simultaneously. Instead, the more precisely a particle’s position is known, the less can be known about its velocity.

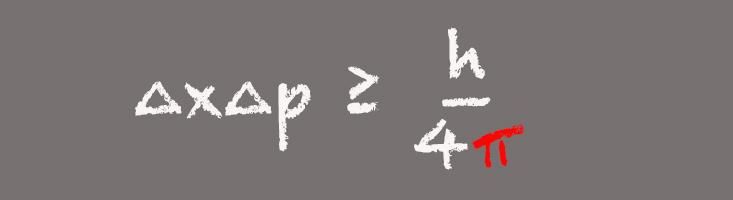
The appearance of pi in Heisenberg’s uncertainty principle makes sense when you realize that in the formula, position and momentum are Fourier transforms of one another, Whitney says. The uncertainty principle is important in the modern world because it describes the behavior of light particles, or photons, in fiber optics communications systems. “What it tells us is that we can’t know both the position and the momentum of photons with extreme precision. You can’t design communications protocols that violate Heisenberg’s uncertainty principle, because they won’t work.”

Stoke’s Law

Stoke’s law calculates the force needed to move a small sphere—that is, a three-dimensional circle—through a viscous fluid at a certain velocity. It has applications in fields ranging from Earth sciences to medicine.

“The law is specifically about the effect of viscosity on a sphere in the fluid,” Whitney says, which is how pi comes into play. As for practical uses of Stoke’s law, look no further than your car. “For decades, the way companies made sure your motor oil had the right viscosity for your car was to literally drop a series of test spheres into the oil and measure the time it takes them to fall through the liquid,” Whitney says. Today, the most common way to measure oil viscosity involves a tool called a capillary tube viscometer, no spheres needed—but it still reports the outcome in units of measurement called centistokes.

Euler’s Formula

Named after Swiss mathematician Leonard Euler, the version of this formula that includes pi gathers some of the most intriguing numbers in mathematics in one place:

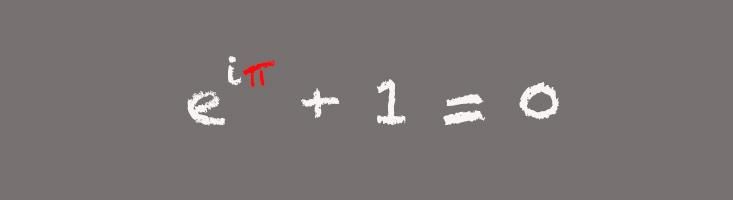
“Everyone just thinks this is incredible. All of these numbers that we consider special appear in one beautiful equation,” Livio says. While this pithy formula can inspire awe in mathematicians, the more useful form of the equation is slightly longer: 

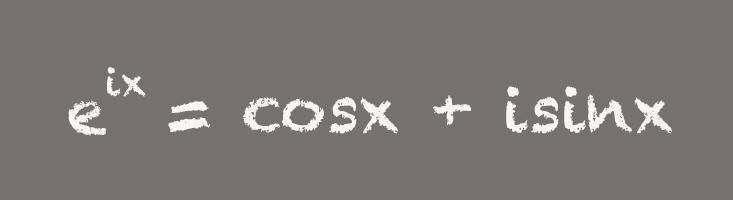
This unpacked version of Euler’s formula is an incredible tool, Whitney says. For example, it’s important for designing electronics that use alternating current, or AC. “Euler’s formula in the expanded form means you can use complex, or imaginary, numbers to analyze and design AC circuits,” Whitney says. That's because in an alternating current circuit, the voltage is a quantity that oscillates over time—typically 60 times per second, for example, in standard U.S. electrical supply. “The full version of Euler's formula teaches how we can use complex numbers as a convenient shorthand for modeling oscillating phenomena," Whitney says.

Einstein’s Field Equations

A core component of his general theory of relativity, Albert Einstein’s field equations describe how gravity from mass and energy create the curvature of space-time.

“Describing that curvature involves geometry, and since the original definition of pi comes from geometry, it’s appearance in this equation is not that surprising,” says Livio. In addition to revealing a fundamental truth about how the universe works, general relativity has many practical applications. For example, the satellites that make up the Global Positioning System used for navigation would be hopelessly out of sync with one another if engineers did not take into account the time dilation effects predicted by the theory.

Ker Than | | READ MORE

Ker Than is a freelance science writer living in the Bay Area. He has written for National Geographic, New Scientist, and Popular Science.