The Mind-Bending Math Behind Spot It!, the Beloved Family Card Game

If you are a parent of children under the age of about 10, the chances are very good that you are acquainted with a game called “Spot It!”

Spot It!, in its distinctive round tin, is hugely popular—it’s in the top ten of Amazon’s list of best-selling card games, right up there with classics such as Uno and Taboo. More than 12 million copies of the game have been sold since its first release in 2009, with more than 500,000 sold each year in the United States alone. It’s frequently used in classrooms, appears on lists of educational games that promote cognitive development, and speech and occupational therapists across the U.S. endorse it. It’s the kind of game that makes you feel like you’re doing something good for your brain when you play it.

The basic structure of the game is this: the deck has 55 cards, with eight symbols on each card, culled from a bank of 57 symbols in total. If you choose any two cards at random, one symbol always matches. The game provides several different ways to play, but they all hinge on the speed with which you spot the match—the two blocks of cheese, the ink spots, the dolphins, the snowmen and so on.

But how—how!?—is it possible that every single card matches another card in just one way?

It’s not magic. It’s math.

**********

The story of Spot It!, first and still published as “Dobble” in Europe, starts in 1850 Britain. At the time, Britain was in the midst of a kind of mathematical renaissance. After a period of relative stagnation during the Georgian era, the reign of Queen Victoria seemed to produce a flowering of mathematical rock-stars, people like Charles Babbage, George Boole, John Venn and Arthur Cayley. This was an era of abstract mathematical philosophy and enquiry, of laying down the mathematical principles that undergird modern-day digital technology—without these guys, modern computing couldn’t exist.

The Reverend Thomas Penyngton Kirkman was not a mathematical rock-star, not exactly. An Anglican clergyman with a bachelor’s degree from Trinity College in Dublin, Kirkman quietly served a small parish in Lancashire, in the north of England, for 52 years. But he was intellectually curious—his son’s obituary of him, after his death in 1895, declared that Kirkman’s chief interests were “the study of pure mathematics, the higher criticism of the Old Testament, and questions of first principles.” About the last two, few records remain. Of the first, however, Kirkman left behind a catalogue of some 60 major papers on everything from group theory to polyhedral—though mostly published in obscure journals, littered with complex and sometimes invented mathematical terminology, and little seen—an under-appreciated legacy, and at least one very interesting problem.

Spot It

Watch on

In 1850, Kirkman submitted a puzzle to “The Ladies and Gentleman’s Diary,” an annual recreational mathematics magazine that took content from both amateurs and professional mathematicians. The question read, “Fifteen young ladies in a school walk out three abreast for seven days in succession: it is required to arrange them daily, so that no two shall walk twice abreast.” Kirkman’s Schoolgirl Problem, as it became known, was a question of combinatorics, a branch of logic that deals with combinations of objects under specified criteria. You’re probably more familiar with combinatorics than you might think—it’s the math principle that informs Sudoku grids. (And if you’ve taken the LSATSs, you’re definitely familiar with it—“Analytical Reasoning” is all about combinatorics.)

Kirkman had actually solved the problem three years prior, when he determined how many schoolgirls he’d need to make the puzzle work. This proof was in response to a question posed in the same magazine in 1844: “Determine the number of combinations that can be made of n symbols, p symbols in each; with this limitation, that no combination of q symbols which may appear in any one of them shall be repeated in any other.” Kirkman extrapolated this as a question of unrepeated pairs in triplets, asking from a certain number of elements, how many unique triplets can you have before you start repeating pairs? In his 2006 book on the Kirkman problem, The Fifteen Schoolgirls, Dick Tahta gives several examples of how the problem might work: “You have seven friends whom you wish to invite to dinner in threes. How many times can you do this before two of them come together a second time?” In that case, n=7, p=3, and q=2.

Notably, Kirkman’s proof was his first mathematical paper, presented in December 1846, when he was already 40 years old. Also, it appeared to be a solution to a problem posed by famous Swiss geometer Jakob Steiner—his “triple system,” a series of unique subsets of three—about six years before Steiner proposed it. But the general solution—the principle behind why it works, and showing that it works all of the time—wouldn’t be figured out until 1968, when mathematician Dijen Ray-Chaudhuri and his then student, Richard Wilson, at Ohio State University, collaborated on a theorem proving it.

“Kirkman was, as far as we know, driven just by curiosity. But as so often happens in mathematics, his ideas turned out to have very wide application. In statistics, Sir Ronald Fisher used them to produce experimental designs which compare any pair of proposed treatments in an optimal fashion. They also arise in the theory of error-correcting codes, as used in communication between computers, satellites, and so on,” writes Peter Cameron, a mathematician at the University of St. Andrews, in an email. “A further application turns out to be card games.”

But not yet. Ray-Chaudhuri and Wilson’s general solution had inspired a wave of interest in Kirkman’s Schoolgirl Problem, not least because its applications in the burgeoning field of coding and computation. Among those it caught up was a young French math enthusiast called Jacques Cottereau. This was 1976, and Cottereau was inspired by relatively new theories of error correcting codes and by the principles of what are called “incomplete balanced blocks,” in which a finite set of elements are arranged into subsets that satisfy certain “balance” parameters, a concept often used in designing experiments.

Cottereau wanted to come up with a model to make the puzzle work in any combination, and he wanted it to be fun. He soon realized that the principles in the solution didn’t have to be numbers or schoolgirls. For his re-imagining of the Schoolgirl Problem, Cottereau designed a “game of insects”: A set of 31 cards with six images of insects, exactly one image shared between each of them. The “game of insects,” a limited version of what Spot It! would become, however, never made it past Cottereau’s living room and spent the next 30 years gathering dust.

Cottereau was neither a professional mathematician nor a games-maker; he was just a hobbyist who had a “passion for this specific domain,” according to Dobble’s co-inventor, Denis Blanchot. Blanchot is also not a mathematician—he is a journalist by trade—but he does enjoy creating and designing games. In 2008, Blanchot came across a few of the cards from the game of insects set—Cottereau is Blanchot’s sister-in-law’s father—and saw in them the seeds of an entertaining game.

“He had the idea to translate it to cards. I turned it into a true game, speed and fun,” Blanchot says via Facebook messenger. They envisioned the game, which they called Dobble, would be for everyone, not just children.

The Math Behind Spot it!

Watch on

​

Blanchot worked on the illustrations for the prototype, a mix of animals, signs, and objects, some of which are still part of the game now, and, after many playtests, they figured out several approaches to gameplay. The game Dobble, so named as a play on the word “double,” launched in France in 2009 under publishers Play Factory, then in Germany in 2010. That same year, Blanchot and Cottereau sold the game to Play Factory. An insert, included in the game’s packaging since 2016, lists Blanchot and Cottereau as the creators, “with help from the Play Factory Team,” though the two are no longer involved with the game at all.

Dobble was released in the U.K. and North America, as Spot It!, in 2011, to fairly immediate success. Asmodee acquired the worldwide rights to the game from Play Factory and U.S. distributor, Blue Orange, in 2015. Now, the game has been published with more than 100 different themes, including the National Hockey League, “hip” (moustaches and bicycles), and Pixar’s Finding Dory. They’ve created versions featuring Spanish and French vocabulary, with the alphabet and numbers, and cards featuring Disney princesses and Star Wars. The initial publishers of the game even once created a version for the French police using roadway symbols—and a wine bottle, says Jon Bruton, buyer for Asmodee Europe: “They said it was a reminder not to drink and drive.”

Ben Hogg, marketing manager for Asmodee Europe, attributed the game’s success—it’s the most popular card game in the U.K. this year—to its ease of play. “People can learn how to play almost immediately. They can play it extraordinarily well, but they can’t master it,” he said. “It’s one of those games you can show people and instantly they get it, they see what’s fun about it.”

**********

But most of the people who play don’t understand exactly why it works. Spot It! may be easy to play, but the math behind it is surprisingly complicated.

Most simply, the game is based on Euclid’s principle that two lines on an infinite, two-dimensional plane will share only a single point in common. In the 18th and 19th centuries, Euclidian geometry informed the basis of modern algebra by way of Rene Descartes assigning these points coordinates, so points were no longer physical locations; they could become numbers and later, systems of numbers. For the purposes of Kirkman’s Schoolgirl Problem, explains Cameron, “think of girls as ‘points’ and groups of three girls as ‘lines.’ Euclid's axiom is satisfied. … The more difficult part of the problem is to divide the 35 groups into 7 clusters of 5 so that each girl occurs once in each cluster. In Euclid's terms, this is like adding the relation of parallelism to the set-up.”

Kirkman’s problem, and therefore Spot It!’s solution, lives in the area of finite geometry. “The most basic of these geometries has q2 points, with q points on each line, where q is the number of elements in the chosen number system or field. A small variant gives q²+q+1 points, with q+1 points on each line,” writes Cameron.

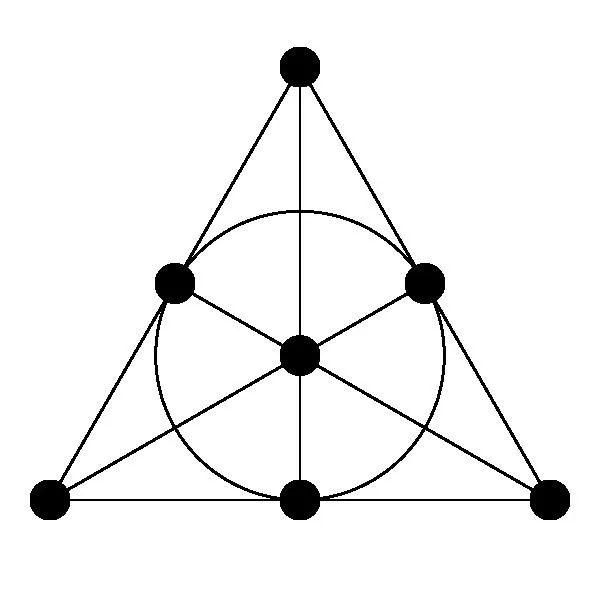
So what does this mean for Spot It? “Let us take one of these geometries and try to turn it into a card game. Each card will be regarded as a point, and will carry a number of symbols representing the lines containing that point. Given any two cards, there will be just one symbol they have in common, corresponding to the unique line through the two points,” Cameron said.

With q being seven in the formula, we can determine that there are 57 points (72+7+1), with eight points (7+1) on each line. “So we can make a pack of 57 cards, with eight symbols on each card, and any two cards having exactly one symbol in common. There, in essence, is the game!” Cameron says.

Notably, however, Spot It! does not contain 57 cards, it only contains 55. One theory about the missing two cards is that the manufacturers used standard card-making machinery, and standard decks of cards contain 55 cards—52 card playing cards, two Jokers, and advertisement. “No problem,” wrote Cameron. “Make 57 cards and lose two of them; the resulting 55 will still have the property that any two share just one symbol. Indeed, no matter how many cards you lose, this property will still hold.”

**********

Of course, you don’t need to understand how it works to enjoy playing the game. But trying to figure it out could be a gateway to understanding or thinking about math in new ways. Before Jon Bruton became a buyer for Asmodee, he was a math teacher at a secondary school in Hampshire, England. He used Dobble in his classrooms, first getting kids to play the game—and then getting them to design their own versions.

“It was one that basically everyone could succeed at an initial level… The idea was a starting point to look at combinatorics and matrices, it was a hook,” he says. “Most kids could design one or two sets, the challenge would be to sit around and ask, how could I actually make this work?”

Figuring out how to make it work, especially beyond sets of two or three, is hard going. So sure, you could buy the game this holiday season—and you’d have a lot of pretty fun thematic options—but what if you made your own?

Linda Rodriguez McRobbie | | READ MORE

Linda Rodriguez McRobbie is an American freelance writer living in London, England. She covers the weird stuff for Smithsonian.com, Boing Boing, Slate, mental_floss, and others, and she's the author of Princesses Behaving Badly.