Can a Statistical Model Accurately Predict Olympic Medal Counts?

If someone asked you to predict the number of medals each country is going to win in this year's Olympics, you'd probably try to identify the favored athletes in each event, then total each country's expected wins to arrive at a result.

Tim and Dan Graettinger, the brothers behind the data mining company Discovery Corps, Inc., have a rather different approach. They ignore the athletes entirely.

Instead, their model for the Sochi games looks at each country's geographic area, GDP per capita, total value of exports and latitude to determine how many medals each country will win. In case you're wondering, it predicts the U.S. will come out on top, with 29 medals in total.

The Graettingers aren't the first to employ this sort of data-driven, top-down approach to predicting medal counts. Daniel Johnson, a Colorado College economics professor, built similar models for the five Olympics between 2000 and 2008—achieving a 94 percent accuracy overall in predicting each country's number of medals—but did not create a model for Sochi.

Dan and Tim are newer to the game. Dan—who typically works on more conventional data mining projects, for example predicting a company's potential customers—first got interested in using models to predict competitions four years ago, during the Vancouver Winter Olympics. "I use data about the past to predict the future all the time," he says. "Every night, they'd show the medal count on TV, and I started wondering if we could predict it."

Even though the performances of individual athletes can vary unpredictably, he reasoned, there might be an overall relationship between a country's fundamental characteristics (its size, climate and amount of wealth, for instance) and the number of medals it would likely take home. This sort of approach wouldn't be able to say which competitor might win a given event, but with enough data, it might be able to accurately predict the aggregate medal counts for each country.

Initially, he and his brother set to work developing a preliminary model for the 2012 London games. To begin, they collected a wide range of different types of data sets, on everything from a country's geography to its history, religion, wealth and political structure. Then, they used regression analyses and other data-crunching methods to see which variables had the closest relationship with historical data on Olympic medals. 

They found that, for the summer games, a model that incorporated a country's gross domestic product, population, latitude and overall economic freedom (as measured by the Heritage Foundation's index) correlated best with each country's medal counts for the previous two summer Olympics (2004 and 2008). But at that point, their preliminary model could only predict which countries would win two or more medals, not the number of medals per country.

They decided to improve it for the Sochi games, but couldn't rely on their previous model, because the countries that are successful in the winter differ so greatly from summer. Their new Sochi model tackles the problem of predicting medal counts in two steps. Because about 90 percent of countries have never won a single Winter Olympics medal (no Middle Eastern, South American, African or Caribbean athlete has ever won), it first separates the ten percent that are likely to win at least one, then predicts how many each one will win.

"Some trends are pretty much what you'd expect—as a country's population gets bigger, there's more of a likelihood that it'll win a medal," Tim says. "Eventually, though, you need some more powerful statistical machinery that can grind through a lot of variables and rank them in terms of which are the most predictive."

Eventually, they came upon a few variables that accurately separate the ninety percent of non medal-winning countries from the ten percent that will likely win: these included migration rate, number of doctors per capita, latitude, gross domestic product and whether the country had won a medal in the previous summer games (no country had ever won a winter medal without winning one the previous summer, in part because the pool of summer winners is so much larger than the winter one). By running this model on the past two Winter Olympics, this model determined which nations took home a medal with 96.5 percent accuracy.

With 90 percent of the countries eliminated, the Graettingers used similar regression analyses to create a model that predicted, retroactively, how many medals each remaining country won. Their analysis found that a slightly different list of variables best fit the historical medal data. These variables along with predictions for the Sochi games are below:

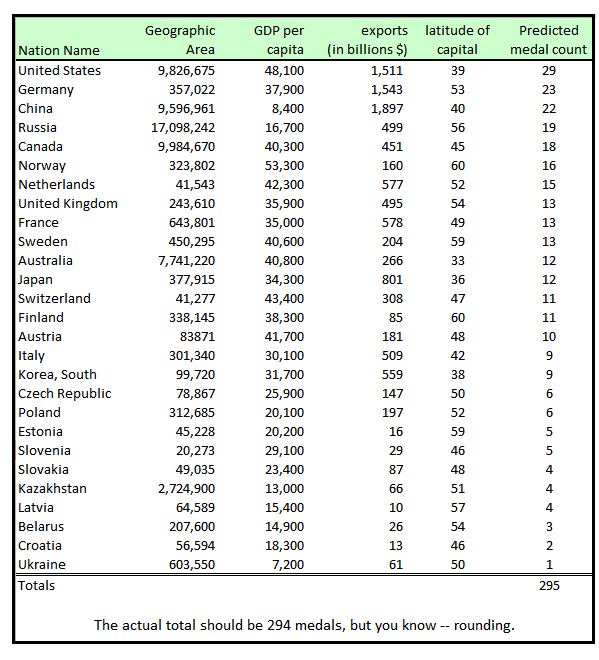
Some of the variables that turned out to be correlative aren't a huge shock—it makes sense that higher-latitude countries do better at the events played during the winter games—but some were more surprising.

"We thought population, not land area, would be important," Dan says. They're unsure why geographic area ends up fitting the historical data more closely, but it might be because a few high population countries that don't win winter medals (like India and Brazil) throw off the data. By using land area instead, the model avoids these countries' outsized influence, but still retains a rough association with population, because on the whole, countries with larger areas do have larger populations.

Of course, the model isn't perfect, even in matching historical data. "Our approach is the 30,000-foot approach. There are variables we can't account for," Tim says. Some countries have repeatedly outperformed the model's predictions (including South Korea, which wins a disproportionate amount of short-track speed skating events) while others consistently underperform (such as the U.K., which seems to do far better at summer events that would be expected, perhaps because—despite its latitude—it gets far more rain than snow).

Additionally, a consistent exception they've found to the model's predictions is that the host country bags more medals than it would otherwise, based simply on the data. Both Italy (during the 2006 Turin games) and Canada (during the 2010 Vancouver games) out-performed the model, with Canada setting its all-time record in winning 14 golds.

Still, based on their statistically-rigorous approach, the Graettingers are confident that on the whole, their model will predict the final medal counts with a relatively high degree of accuracy.

How do their predictions compare to those of experts that use more conventional strategies? The experts don't differ dramatically, but they do have a few traditionally-successful countries (Norway, Canada, Russia) winning higher numbers of medals, along with a few others (China, the Netherlands, Australia) each winning a few fewer.

To date, the Graettingers haven't put down any bets on their predictions, but they do plan on comparing their model's output to the betting odds just before the games kick off. If they see any discrepancies they'd like to exploit, they might end up putting their money where their mouth is.

Joseph Stromberg | | READ MORE

Joseph Stromberg was previously a digital reporter for Smithsonian.